Công thức logarit
Logarit là một phép toán nghịch đảo của phép lũy thừa. Nói một cách đơn giản, logarit trả lời câu hỏi: "Số mũ mà ta cần nâng một số cơ bản lên để thu được một số cụ thể là bao nhiêu?".
Ví dụ:
Nếu ta có phép tính: 10^2 = 100 Thì ta có thể viết lại dưới dạng logarit: log10(100) = 2
Trong đó:
log: Ký hiệu của logarit
10: Cơ số (số mà ta nâng lên lũy thừa)
100: Số cần tìm logarit
2: Logarit của 100 với cơ số 10, tức là số mũ mà ta cần nâng 10 lên để được 100.
Các loại logarit thường gặp
Logarit thập phân: Có cơ số là 10, thường được viết gọn là log (log10).
Logarit tự nhiên: Có cơ số là số e (một hằng số đặc biệt xấp xỉ 2.71828), thường được viết là ln.

Logarit Các công thức logarit cơ bản
logₐ(1) = 0: Bất kỳ số dương nào khác 1 nâng lên mũ 0 đều bằng 1.
logₐ(a) = 1: a nâng lên mũ 1 bằng chính nó.
logₐ(a^n) = n: Đây là định nghĩa cơ bản của logarit.
a^logₐ(x) = x: Đây là phép toán nghịch đảo của logarit.
logₐ(b × c) = logₐ(b) + logₐ(c): Logarit của một tích bằng tổng các logarit.
logₐ(b / c) = logₐ(b) - logₐ(c): Logarit của một thương bằng hiệu các logarit.
logₐ(b^n) = n × logₐ(b): Logarit của một lũy thừa bằng tích của số mũ với logarit của cơ số.
logₐ(√b) = (1/2) × logₐ(b): Logarit của căn bậc hai của một số bằng một nửa logarit của số đó.
Đổi cơ số: logₐ(b) = logₓ(b) / logₓ(a)
Giải thích các công thức logarit
Công thức 5 và 6: Các công thức này cho phép ta đưa phép nhân và phép chia trong logarit về dạng tổng và hiệu của các logarit đơn giản hơn.
Công thức 7: Công thức này cho phép ta đưa lũy thừa ra ngoài logarit.
Công thức 8: Đây là trường hợp đặc biệt của công thức 7 với n = 1/2.
Công thức 9: Công thức đổi cơ số cho phép ta chuyển đổi giữa các logarit có cơ số khác nhau.
Ứng dụng của logarit
Giải phương trình mũ: Logarit được sử dụng để đưa phương trình mũ về dạng phương trình bậc nhất hoặc bậc hai.
Tính toán lãi kép: Logarit được sử dụng để tính số năm cần thiết để một khoản tiền gửi đạt được một giá trị nhất định.
Đo lường độ lớn: Logarit được sử dụng để đo độ lớn của các đại lượng như độ pH, độ lớn âm thanh (đề-xi-ben), độ sáng...
Phân tích độ phức tạp của thuật toán: Logarit được sử dụng để đánh giá hiệu suất của các thuật toán.
Ví dụ
Tính log₂(8):
Ta có: 2^3 = 8
Vậy log₂(8) = 3
Tính log₁₀(0.01):
Ta có: 10^-2 = 0.01
Vậy log₁₀(0.01) = -2

Công thức về logaritHàm số logarit là một khái niệm quan trọng trong toán học, đặc biệt trong lĩnh vực giải tích. Nó là hàm ngược của hàm số mũ và có vai trò quan trọng trong việc giải các phương trình mũ, tính toán lãi kép, đo lường độ lớn của các đại lượng trong tự nhiên và khoa học.
Định nghĩa
Hàm số logarit cơ số a của x, ký hiệu là logₐ(x), được định nghĩa như sau:
Nếu a^y = x (với a > 0, a ≠ 1 và x > 0) thì y = logₐ(x)
Trong đó:
a: Cơ số (phải dương và khác 1)
x: Số cần tìm logarit (phải dương)
y: Logarit của x với cơ số a
Ví dụ:
log₂(8) = 3 vì 2³ = 8
log₁₀(100) = 2 vì 10² = 100
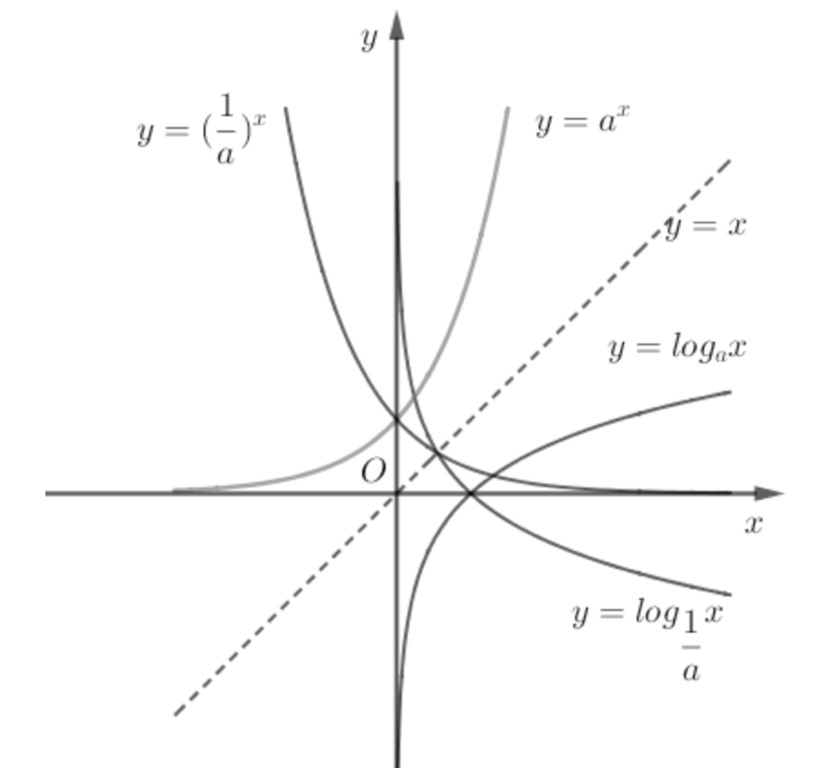
Đồ thị hàm số logarit
Đồ thị của hàm số logarit có dạng như sau:
Khi a > 1: Đồ thị hàm số đi qua điểm (1, 0) và tăng dần.
Khi 0 < a < 1: Đồ thị hàm số đi qua điểm (1, 0) và giảm dần.
Tính chất của hàm số logarit
Tập xác định: (0; +∞)
Tập giá trị: R
Đồng biến: Khi a > 1
Nghịch biến: Khi 0 < a < 1
Không có cực trị
Đồ thị luôn cắt trục Ox tại điểm (1, 0)
Các loại logarit thường gặp
Logarit thập phân: Có cơ số là 10, thường được viết gọn là log (log₁₀).
Logarit tự nhiên: Có cơ số là số e (một hằng số đặc biệt xấp xỉ 2.71828), thường được viết là ln.
Logarit nhị phân: Có cơ số là 2, thường được sử dụng trong khoa học máy tính.
Ứng dụng của hàm số logarit
Giải phương trình mũ: Logarit được sử dụng để đưa phương trình mũ về dạng phương trình bậc nhất hoặc bậc hai.
Tính toán lãi kép: Logarit được sử dụng để tính số năm cần thiết để một khoản tiền gửi đạt được một giá trị nhất định.
Đo lường độ lớn: Logarit được sử dụng để đo độ lớn của các đại lượng như độ pH, độ lớn âm thanh (đề-xi-ben), độ sáng...
Phân tích độ phức tạp của thuật toán: Logarit được sử dụng để đánh giá hiệu suất của các thuật toán.
Hàm số logaritBài tập cơ bản
Tính giá trị của các biểu thức sau:
log₂(8)
log₁₀(0.01)
ln(e²)
log₃(√27)
Giải các phương trình logarit sau:
log₂(x + 1) = 3
log₃(2x - 1) = 2
log₅(x²) = 4
Vẽ đồ thị hàm số:
y = log₂(x)
y = log₀.₅(x)
Bài tập nâng cao
Chứng minh các đẳng thức:
logₐ(b) . logᵦ(c) = logₐ(c)
logₐ(bⁿ) = n.logₐ(b)
Giải các phương trình logarit phức tạp:
log₂(x²) + log₂(x - 1) = 5
log₃(x + 1) + log₃(x - 2) = 1
Tìm giá trị lớn nhất, nhỏ nhất của hàm số:
y = log₂(x² - 4x + 5) trên đoạn [1; 3]
Bài toán ứng dụng
Một chất phóng xạ có chu kỳ bán rã là T năm. Sau thời gian t năm, lượng chất phóng xạ còn lại là A(t) = A₀.(1/2)^(t/T), trong đó A₀ là lượng chất phóng xạ ban đầu. Hãy tìm thời gian cần thiết để lượng chất phóng xạ giảm đi một nửa.
Bài tập vận dụng cao
Giải bất phương trình logarit:
log₂(x² - 3x) > 2
log₃(x + 1) ≤ log₃(9 - x²)
Khảo sát và vẽ đồ thị hàm số:
y = log₂(x - 1) + 2
y = -log₃(x + 2)
Bài toán liên quan đến hàm số mũ và logarit
Giải hệ phương trình:
2ˣ + 3ʸ = 7
3ˣ - 2ʸ = 2
Trên đây là một số thông tin về công thức logarit. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.