Diện tích tam giác vuông cân
Trường hợp đặc biệt của tam giác vuông
Tam giác vuông cân là một trường hợp đặc biệt của tam giác vuông, trong đó hai cạnh góc vuông bằng nhau. Giả sử ta có tam giác ABC vuông cân tại A, khi đó AB = AC và góc A = 90°. Chính tính chất này khiến tam giác vuông cân vừa có yếu tố đối xứng, vừa có mối liên hệ chặt chẽ giữa cạnh, góc và đường cao.
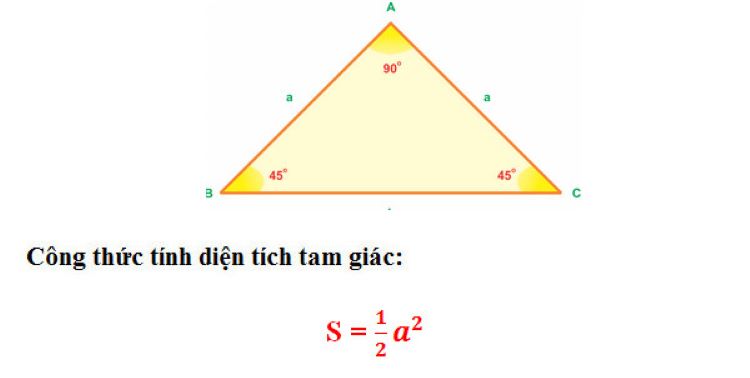
Tam giác vuông cân
Một tam giác vuông cân có hai góc nhọn còn lại bằng nhau, mỗi góc đều bằng 45 độ. Vì vậy, nó được xem là một nửa của hình vuông khi chia theo đường chéo. Khi ta kẻ đường cao từ đỉnh góc vuông xuống cạnh huyền, đường này đồng thời là trung tuyến, phân giác và cũng là trục đối xứng của tam giác. Đó là lý do vì sao các bài toán liên quan đến tam giác vuông cân thường dễ quy đổi sang hình vuông để suy luận.
Nếu ký hiệu cạnh góc vuông là a, thì cạnh huyền c của tam giác vuông cân sẽ có độ dài bằng a x sqrt(2). Mối quan hệ này bắt nguồn từ định lý Pythagore: c^2 = a^2 + a^2 = 2a^2, nên c = a x sqrt(2). Đây là yếu tố quan trọng giúp ta dễ dàng chuyển đổi giữa cạnh góc vuông và cạnh huyền trong quá trình tính toán diện tích hoặc các đại lượng khác.
Tam giác vuông cân không chỉ tồn tại trên mặt phẳng mà còn xuất hiện nhiều trong hình học không gian, ví dụ như mặt phẳng cắt vuông góc trong hình chóp, hay tiết diện của hình nón khi chiếu sáng tạo thành bóng tam giác đối xứng. Vì vậy, việc nắm chắc cấu trúc và công thức của nó là nền tảng để học tốt các phần kiến thức cao hơn.

Tam giác vuông cân có tính đối xứng giúp dễ dàng suy luận và áp dụng công thức
Công thức cơ bản
Để tính diện tích của tam giác vuông cân, ta bắt đầu từ công thức tổng quát tính diện tích của tam giác vuông. Diện tích của một tam giác vuông bất kỳ được xác định bằng nửa tích của hai cạnh góc vuông. Ký hiệu hai cạnh góc vuông là a và b, ta có S = 1/2 x a x b.
Với tam giác vuông cân, hai cạnh góc vuông bằng nhau, nên a = b. Khi thay vào công thức, ta thu được:
S = 1/2 x a^2
Đây là công thức cơ bản nhất để tính diện tích của tam giác vuông cân.
Công thức biến thể
Nếu đề bài cho cạnh huyền c thay vì cạnh góc vuông, ta có thể chuyển đổi sang công thức khác. Vì c = a x sqrt(2), nên a = c / sqrt(2). Thay vào công thức diện tích, ta được S = 1/2 x (c^2 / 2) = 1/4 x c^2. Như vậy, diện tích tam giác vuông cân cũng có thể tính dễ dàng khi chỉ biết cạnh huyền.
Ngoài ra, khi tam giác vuông cân nội tiếp trong một đường tròn, cạnh huyền chính là đường kính của đường tròn ngoại tiếp. Khi đó, bán kính R = c / 2. Từ công thức S = 1/4 x c^2, ta có thể biểu diễn lại theo bán kính là S = R^2. Đây là một công thức rất thú vị, cho thấy diện tích tam giác vuông cân tỉ lệ thuận với bình phương bán kính của đường tròn ngoại tiếp nó.
Một cách chứng minh khác mang tính trực quan hơn là tưởng tượng tam giác vuông cân như một nửa hình vuông. Nếu ta dựng hình vuông có cạnh dài a, diện tích hình vuông là a^2. Khi ta cắt hình vuông đó theo đường chéo, ta được hai tam giác vuông cân bằng nhau. Vì diện tích bị chia đôi, diện tích mỗi tam giác là S = 1/2 x a^2. Cách chứng minh này không chỉ giúp học sinh dễ nhớ mà còn thể hiện rõ mối quan hệ đối xứng giữa hai hình.
Tam giác vuông cân là nửa của hình vuông, nên diện tích bằng nửa diện tích hình vuông cùng cạnh
Tam giác vuông cân không chỉ có diện tích phụ thuộc vào cạnh mà còn có mối quan hệ mật thiết với đường cao. Nếu ta kẻ đường cao từ đỉnh góc vuông xuống cạnh huyền, ký hiệu là h, thì trong tam giác vuông cân, đường cao cũng đồng thời là đường trung tuyến và đường phân giác.
Từ các hệ thức lượng trong tam giác vuông, ta có h = a x sqrt(2) / 2. Khi đó, diện tích của tam giác có thể được biểu diễn dưới dạng S = 1/2 x c x h. Thay c = a x sqrt(2) và h = a x sqrt(2) / 2 vào, ta thu được S = 1/2 x a^2. Việc này cho thấy rằng dù ta dùng cạnh góc vuông, cạnh huyền hay đường cao để tính, kết quả diện tích luôn không đổi.
Nếu ta xét mối quan hệ giữa diện tích và chu vi, ta có thể suy luận thêm rằng khi a càng lớn, diện tích tam giác tăng theo bình phương của cạnh, trong khi chu vi chỉ tăng tuyến tính. Điều đó có nghĩa là diện tích phát triển nhanh hơn nhiều so với độ dài chu vi, minh chứng cho sự “mở rộng” mạnh mẽ của tam giác vuông cân khi phóng to tỉ lệ.

Trong tam giác vuông cân, đường cao đồng thời là trung tuyến và phân giác
Công thức tính diện tích của tam giác vuông cân không chỉ xuất hiện trong bài tập toán học mà còn được ứng dụng rộng rãi trong đời sống và kỹ thuật. Trong kiến trúc, mái nhà hình chữ A hoặc khung cửa sổ tam giác thường được thiết kế dựa trên cấu trúc tam giác vuông cân để đảm bảo tính đối xứng và vững chắc. Việc tính toán diện tích giúp xác định lượng vật liệu cần thiết, chẳng hạn như gỗ, kính hoặc thép.
Ví dụ, một cửa sổ tam giác vuông cân có cạnh góc vuông dài 1,2 m, người thợ muốn biết diện tích kính cần lắp. Áp dụng công thức S = 1/2 x a^2, ta có S = 1/2 x 1,2^2 = 0,72 m^2. Kết quả này giúp tính toán chi phí và cắt vật liệu chính xác mà không gây lãng phí.
Diện tích tam giác vuông cân không chỉ là công thức đơn giản S = 1/2 x a^2, mà còn là một hệ thống kiến thức hình học liên kết chặt chẽ giữa cạnh, góc, đường cao và đường tròn. Hiểu sâu bản chất của nó giúp ta không chỉ tính toán chính xác mà còn phát triển tư duy hình học trực quan, logic và sáng tạo hơn.