Hệ thức lượng trong tam giác vuông
Hiểu đúng về tam giác vuông
Tam giác vuông là tam giác có một góc bằng 90°. Đây là dạng hình học quen thuộc và được ứng dụng nhiều nhất trong các bài toán đo đạc, vật lý, kỹ thuật hay xây dựng. Trong tam giác vuông, các cạnh và góc có mối quan hệ đặc biệt được gọi là hệ thức lượng tam giác vuông – nền tảng cho nhiều định lý nổi tiếng như định lý Pythagore và các công thức lượng giác.
Khái niệm hệ thức lượng
Hệ thức lượng là tập hợp các công thức biểu diễn mối liên hệ giữa cạnh, đường cao, đường trung tuyến, góc và bán kính đường tròn nội – ngoại tiếp của tam giác vuông. Việc hiểu và vận dụng các hệ thức này giúp ta tính được các đại lượng chưa biết khi chỉ biết một vài yếu tố cơ bản.

Tam giác vuông có mối quan hệ đặc biệt giữa cạnh, góc và đường cao
Hệ thức giữa các cạnh của tam giác vuông
Trong tam giác vuông ABC có góc vuông tại A, ta có công thức nổi tiếng nhất:
c^2 = a^2 + b^2
Trong đó, c là cạnh huyền, a và b là hai cạnh góc vuông. Đây chính là định lý Pythagore, cho phép tính cạnh còn lại khi biết hai cạnh bất kỳ.
Ngoài ra, khi cần tính ngược lại, ta có thể sử dụng các công thức:
- a = sqrt(c^2 - b^2)
- b = sqrt(c^2 - a^2)
Hệ thức giữa cạnh và đường cao
Đường cao trong tam giác vuông được hạ từ đỉnh góc vuông xuống cạnh huyền. Ký hiệu AH là đường cao, H là chân đường cao. Khi đó, ta có các hệ thức:
- h^2 = m x n
- a^2 = c x m
- b^2 = c x n
Trong đó:
- h là đường cao,
- m và n là hai đoạn thẳng trên cạnh huyền tạo bởi đường cao.
Các công thức này cho phép tính nhanh độ dài đường cao hoặc các đoạn chia trên cạnh huyền khi biết các cạnh khác.

Đường cao trong tam giác vuông giúp thiết lập mối quan hệ quan trọng giữa các cạnh
Đường trung tuyến ứng với cạnh huyền
Đường trung tuyến AM nối từ góc vuông A đến trung điểm M của cạnh huyền BC có độ dài bằng một nửa cạnh huyền, tức là:
AM = 1/2 x c
Đây là tính chất đặc biệt chỉ có ở tam giác vuông. Nhờ đó, ta có thể dễ dàng xác định trung điểm cạnh huyền hoặc dùng trong các bài toán dựng hình.
Bán kính đường tròn nội tiếp và ngoại tiếp
Với tam giác vuông có hai cạnh góc vuông là a và b, cạnh huyền là c:
- Bán kính đường tròn nội tiếp (r): r = (a + b - c) / 2
- Bán kính đường tròn ngoại tiếp (R): R = c / 2
Hai công thức này được sử dụng phổ biến trong bài tập hình học không gian hoặc tính diện tích nhanh qua các yếu tố liên quan đến đường tròn.
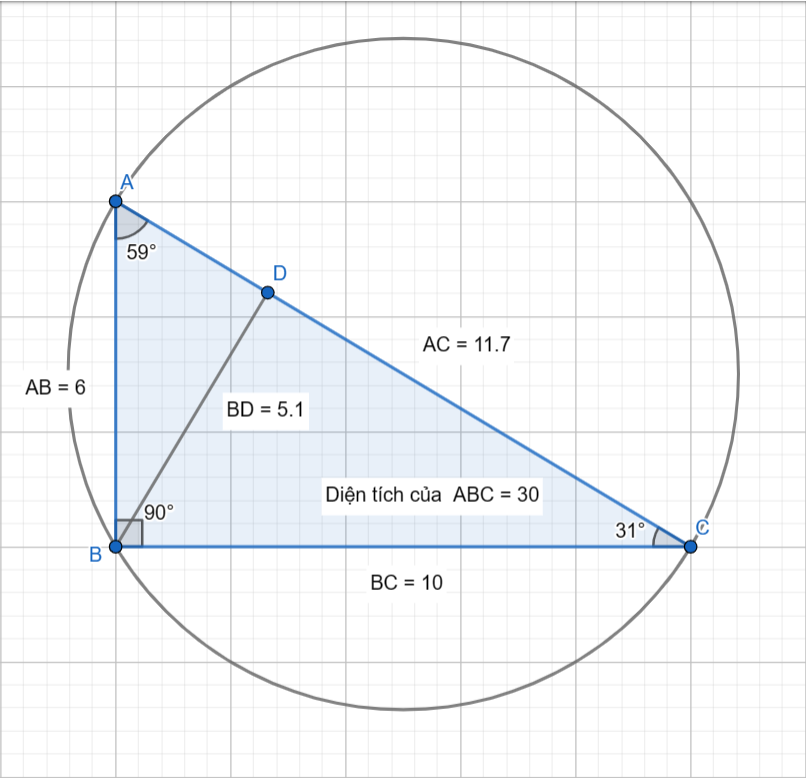
Mối liên hệ giữa các đường tròn và cạnh của tam giác vuông
Tính chiều cao của vật thể
Giả sử bạn muốn đo chiều cao của một tòa nhà nhưng không thể leo lên đỉnh, bạn có thể đo độ dài bóng của tòa nhà và góc tạo bởi tia nắng mặt trời. Khi đó, nhờ hệ thức lượng tam giác vuông, chiều cao h của tòa nhà được tính theo công thức:
h = L x tan(alpha)
Trong đó, L là chiều dài bóng và alpha là góc giữa mặt đất và tia nắng.
Xác định khoảng cách giữa hai điểm
Trong kỹ thuật hoặc bản đồ học, hệ thức lượng giúp xác định khoảng cách giữa hai vị trí khi biết tọa độ theo trục x, y:
d = sqrt[(x2 - x1)^2 + (y2 - y1)^2]
Đây chính là hệ quả trực tiếp của định lý Pythagore, ứng dụng nhiều trong tính toán GPS, đo đạc và lập trình đồ họa.
Liên hệ với lượng giác
Từ hệ thức lượng trong tam giác vuông, ta có thể định nghĩa các tỉ số lượng giác:
- sin(alpha) = đối / huyền
- cos(alpha) = kề / huyền
- tan(alpha) = đối / kề
- cot(alpha) = kề / đối
Nhờ đó, học sinh có thể chuyển từ hình học thuần túy sang bài toán lượng giác dễ dàng hơn.
Hệ thức lượng trong tam giác vuông có ứng dụng rộng rãi trong đời sống và kỹ thuật
Thay vì học thuộc lòng từng công thức, bạn có thể ghi nhớ theo “câu chuyện” của tam giác vuông. Hãy tưởng tượng cạnh huyền là “cha”, hai cạnh góc vuông là “con”. Khi hai “con” cùng lớn (bình phương), hợp lại sẽ bằng “cha” (cạnh huyền bình phương):
a^2 + b^2 = c^2
Khi có đường cao, hãy nhớ rằng “cha sinh hai con nhỏ” – tức cạnh huyền chia thành hai đoạn m và n – thì:
h^2 = m x n
Và khi tam giác ấy nằm gọn trong đường tròn, cha ôm lấy cả ba, nên bán kính ngoại tiếp R = c / 2.
Cách ghi nhớ bằng hình ảnh và câu chuyện sẽ giúp học sinh không còn “sợ” công thức mà hiểu được bản chất của mối quan hệ hình học.
Hệ thức lượng trong tam giác vuông là nền tảng quan trọng của hình học phẳng, đồng thời là chiếc cầu nối dẫn đến kiến thức lượng giác và hình học không gian. Việc nắm vững các công thức này không chỉ giúp giải nhanh bài tập mà còn hiểu sâu mối liên hệ giữa các yếu tố trong một tam giác.
Khi học, hãy nhớ rằng công thức chỉ là “ngôn ngữ” mô tả quy luật hình học. Một khi bạn đã hiểu quy luật ấy, việc áp dụng hệ thức lượng sẽ trở nên tự nhiên và dễ dàng – giống như cách mà một tam giác vuông luôn vững vàng trên nền tảng của nó.
Trong thực tế, tam giác vuông là biểu tượng của sự cân bằng - yếu tố mà cả toán học lẫn nghệ thuật đều hướng đến. Vì thế, khi bạn nhìn thấy một mái nhà, một tấm kính hay một họa tiết gấp giấy origami, hãy thử nhớ lại công thức nhỏ bé ấy – bởi nó chính là nền tảng của rất nhiều điều lớn lao trong thế giới hình học quanh ta.