Số vô tỉ là gì?
Trong toán học, số vô tỉ là những số không thể biểu diễn dưới dạng phân số với tử và mẫu là số nguyên. Nói cách khác, nếu một số không thể viết được dưới dạng a/b (Số Vô Tỉ Là Gì? Cách Nhận Biết, Ví Dụ Và Phân Biệtvới a, b là số nguyên và b ≠ 0) thì số đó là số vô tỉ.
Một cách định nghĩa khác: số vô tỉ là số thập phân vô hạn không tuần hoàn. Tức là phần thập phân của nó kéo dài mãi mãi, không xuất hiện chu kỳ lặp lại.
Ví dụ:
√ 2=1.4142135623… (không bao giờ kết thúc và không có chu kỳ lặp lại)
π=3.1415926535…
e=2.7182818284…
Đây đều là các số vô tỉ nổi tiếng trong toán học, được sử dụng rộng rãi trong nhiều lĩnh vực như hình học, giải tích, vật lý và kỹ thuật.
Điểm đặc biệt của số vô tỉ là chúng nằm chen giữa các số hữu tỉ, tạo nên tính liên tục của trục số thực. Nhờ có số vô tỉ, tập hợp số thực (R) mới trở nên đầy đủ, bao gồm cả số hữu tỉ và vô tỉ.
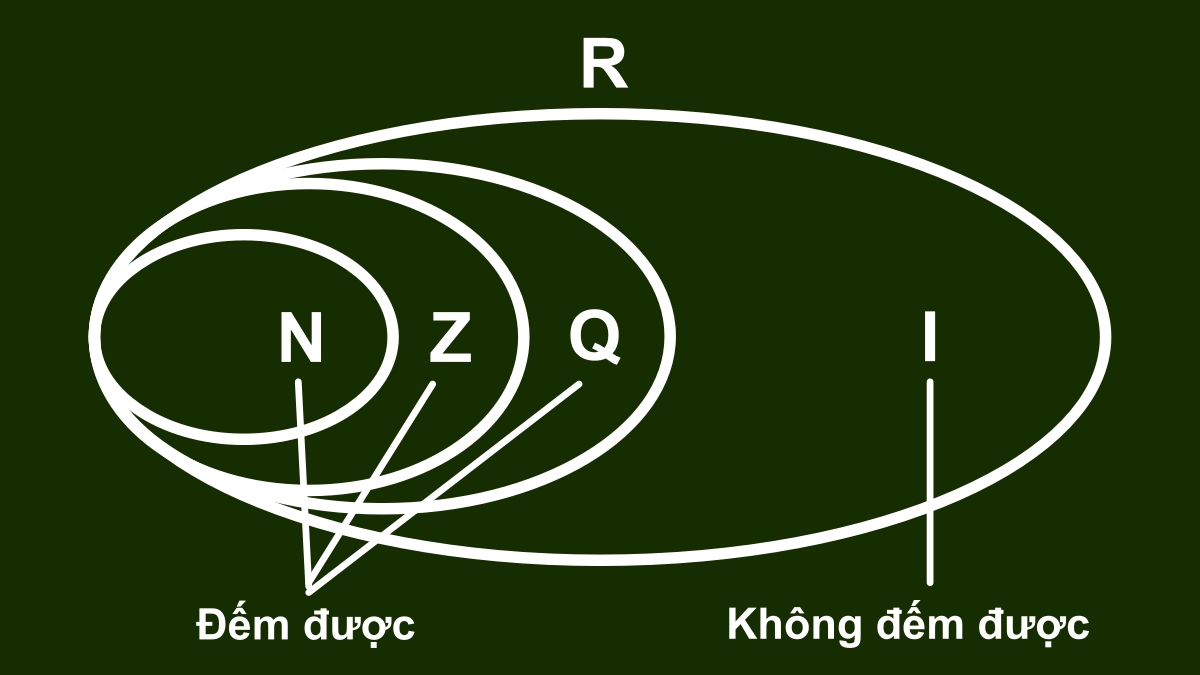Định nghĩa số vô tỉNhiều người thường nhầm lẫn giữa số hữu tỉ và số vô tỉ, do cả hai đều có thể viết ở dạng thập phân. Tuy nhiên, bản chất của chúng rất khác nhau.
Số hữu tỉ là gì?
Số hữu tỉ là số có thể viết được dưới dạng a/b (với a, b ∈ Z và b ≠ 0).
Khi biểu diễn dưới dạng thập phân, số hữu tỉ hoặc hữu hạn, hoặc vô hạn nhưng có chu kỳ lặp lại.
Ví dụ:
1/2=0.5 (thập phân hữu hạn)
1/3=0.3333… (vô hạn tuần hoàn, với chu kỳ là “ 3” )
-7/4=-1.75
Số vô tỉ là gì?
Ngược lại, số vô tỉ không thể viết dưới dạng a/b.
Phần thập phân của nó vô hạn và không tuần hoàn — nghĩa là các chữ số sau dấu phẩy không có quy luật lặp lại nào.
Ví dụ:
√ 3=1.7320508075…
π=3.1415926535…
e=2.7182818284…
Bảng so sánh nhanh
Tiêu chí | Số hữu tỉ | Số vô tỉ |
Cách biểu diễn | Dạng phân số a/b với a, b ∈ Z, b ≠ 0 | Không thể biểu diễn dạng a/b |
Dạng thập phân | Hữu hạn hoặc tuần hoàn | Vô hạn, không tuần hoàn |
Ví dụ | 1/2, 5, -3, 0.75, 2.3333… | √ 2, π, e, √ 3 |
Thuộc tập hợp | Q (tập hợp số hữu tỉ) | R \ Q (phần bù của Q trong R) |
Như vậy, mọi số thực đều là số hữu tỉ hoặc số vô tỉ, không có ngoại lệ. Hai loại số này bổ sung cho nhau để tạo nên trục số thực hoàn chỉnh.
Số vô tỉ trong toán họcĐể xác định xem một số có phải là số vô tỉ hay không, ta có thể dựa vào các dấu hiệu sau:
Không thể viết được dưới dạng phân số
Nếu không tồn tại hai số nguyên a, b (b ≠ 0) sao cho số đó bằng a/b, thì đó là số vô tỉ.
Ví dụ: √ 2 không thể biểu diễn dưới dạng phân số chính xác nào → là số vô tỉ.
Dạng thập phân vô hạn không lặp lại
Một số có phần thập phân kéo dài mãi mà không có chu kỳ lặp lại, chính là số vô tỉ.
Ví dụ:
π=3.1415926535…
e=2.7182818284…
Các căn bậc hai, ba, ... không hoàn hảo
Nếu một số là căn bậc hai, bậc ba, … của một số nguyên nhưng không ra kết quả chính xác, thì đó là số vô tỉ.
Ví dụ:
√ 2 (vì 2 không phải là bình phương của số nguyên nào) → vô tỉ
√ 4=2 (vì 2 là số nguyên) → hữu tỉ
Tổng quát:
Nếu n không phải là số chính phương, thì √ n là số vô tỉ.
Nếu n không phải là lập phương hoàn hảo, thì ∛n là số vô tỉ.
Các hằng số đặc biệt
Một số hằng số toán học nổi tiếng luôn là số vô tỉ:
π (chu vi/đường kính hình tròn)
e (cơ số của logarit tự nhiên)
φ (tỷ lệ vàng, khoảng 1.6180339… )
Dùng phép chứng minh phản chứng
Phương pháp phổ biến để chứng minh một số là vô tỉ là chứng minh phản chứng.
Ví dụ, chứng minh √ 2 là vô tỉ như sau:
Giả sử √ 2 là hữu tỉ → tồn tại a, b nguyên tố cùng nhau sao cho √ 2=a/b.
→ 2=a²/ b² → a² =2b² .
Suy ra a² là số chẵn → a chẵn → a=2k.
Thay vào: (2k)² =2b² → 4k² =2b² → b² =2k² → b cũng chẵn.
→ a và b đều chẵn, mâu thuẫn với giả thiết ban đầu “ nguyên tố cùng nhau” .
→ √ 2 là vô tỉ.
Phép chứng minh này là một trong những ví dụ kinh điển trong toán học sơ cấp.
Học sinh trong giờMặc dù khái niệm “ vô tỉ” nghe có vẻ trừu tượng, nhưng số vô tỉ xuất hiện ở khắp nơi trong cuộc sống thực tế.
Trong hình học
Số vô tỉ thường xuất hiện khi tính độ dài đường chéo, cạnh, bán kính…
Ví dụ:
Độ dài đường chéo hình vuông cạnh 1 là √ 2.
Trong tam giác vuông có cạnh góc vuông 1 và 2, cạnh huyền=√ 5.
Bán kính đường tròn có chu vi C=2πr → π là số vô tỉ.
Trong lượng giác và hình tròn
Các công thức lượng giác thường sử dụng π (số vô tỉ):
sin(π/2)=1, cos(π)=-1, v.v…
Khi đo góc, chu vi, diện tích hình tròn, ta luôn gặp số π.
Trong giải tích và logarit
Số e là cơ sở cho logarit tự nhiên (ln) và hàm mũ (eˣ).
e và π còn xuất hiện trong công thức nổi tiếng:
e^(iπ)+1=0 — được coi là “ phương trình đẹp nhất trong toán học” .
Trong vật lý và kỹ thuật
Các mô hình dao động, sóng, điện xoay chiều… đều dùng sin, cos có liên quan đến π.
Số e xuất hiện trong sự phân rã phóng xạ, tăng trưởng dân số, lãi suất kép, v.v…
Trong nghệ thuật và kiến trúc
Tỷ lệ vàng φ ≈ 1.618… là số vô tỉ được sử dụng để tạo nên sự hài hòa trong nghệ thuật, hội họa và kiến trúc.
Nhiều công trình nổi tiếng như Đền Parthenon (Hy Lạp) hay Kim tự tháp Ai Cập đều được xây dựng dựa trên tỷ lệ này.
Số vô tỉ là một phần không thể thiếu của thế giới toán học. Chúng không thể biểu diễn bằng phân số, có phần thập phân vô hạn không lặp lại, và góp phần tạo nên tính liên tục của trục số thực.
Từ những hằng số như √ 2, π, e, đến các ứng dụng trong hình học, giải tích, kỹ thuật và nghệ thuật — số vô tỉ hiện diện ở khắp nơi. Việc hiểu rõ bản chất và cách phân biệt số vô tỉ giúp chúng ta nắm vững nền tảng toán học, phục vụ tốt cho việc học và ứng dụng trong thực tế.