Diện tích tam giác vuông cân
Lý thuyết về diện tích của tam giác vuông cân
Tam giác vuông cân là một tam giác:
Có một góc vuông (90∘).
Hai cạnh góc vuông bằng nhau.
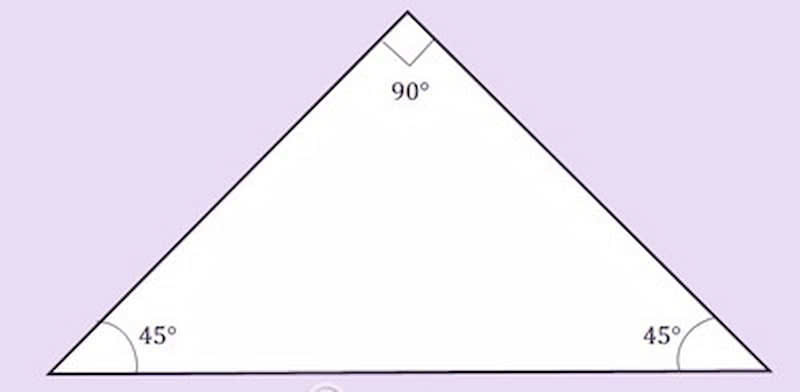Định nghĩa tam giác vuông cânHai góc còn lại đều bằng 45∘, vì tổng ba góc trong tam giác luôn bằng 180∘.
Hai cạnh góc vuông bằng nhau được gọi là đáy và chiều cao của tam giác.
Cạnh huyền (cạnh dài nhất đối diện góc vuông) có độ dài bằng a√2, với a là độ dài một cạnh góc vuông.
Diện tích của tam giác vuông cân được tính theo công thức:
S=1 / 2 × đáy x chiều cao
Vì trong tam giác vuông cân:
Đáy = Chiều cao = a (độ dài một cạnh góc vuông), nên:
S = (1/2) × a × a = a² / 2
Lưu ý:
Nếu biết diện tích S, có thể tính độ dài cạnh góc vuông bằng cách:
a = √(2 × S)
Quan hệ giữa các cạnh:
Hai cạnh góc vuông bằng nhau: a₁ = a₂ = a
Cạnh huyền: aₕ = a√2
Đường cao từ đỉnh góc vuông:
Đường cao từ đỉnh góc vuông chia cạnh huyền thành hai đoạn bằng nhau.
Đường cao cũng bằng: h = (a√2) / 2
Liên hệ với các hình học khác:
Hai tam giác vuông cân bằng nhau được tạo ra khi cắt đôi hình vuông theo đường chéo.
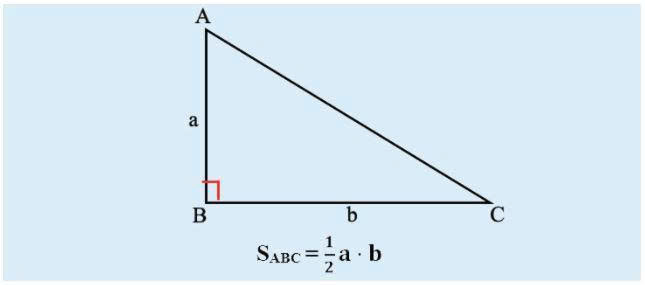Một số tính chất quan trọng của tam giác vuông cânDưới đây là một số bài tập áp dụng về diện tích của tam giác vuông cân, giúp bạn thực hành và củng cố kiến thức:
Bài tập 1: Tính diện tích tam giác vuông cân
Cho một tam giác vuông cân có độ dài cạnh góc vuông là 6 cm. Tính diện tích của tam giác này.
Hướng dẫn giải:
Công thức diện tích của tam giác vuông cân: S = (1/2) × a × a = (a²) / 2
Thay a=6:
S = 6² / 2 = 36 / 2 = 18 cm²
Kết quả: Diện tích tam giác là 18 cm²
Bài tập 2: Tính độ dài cạnh huyền
Cho tam giác vuông cân có diện tích là 32 cm². Tính độ dài của cạnh huyền.
Hướng dẫn giải:
Công thức diện tích của tam giác vuông cân: S = a² / 2
Biết diện tích S=32, thay vào công thức: 32 = (a²) / 2 ⇒ a² = 64 ⇒ a = √64 = 8
Cạnh huyền aₕ của tam giác vuông cân được tính bằng: aₕ = a√2 = 8√2 ≈ 11.31 cm
Kết quả: Cạnh huyền có độ dài khoảng 11.31cm.
Bài tập 3: Tính diện tích từ cạnh huyền
Cho tam giác vuông cân có cạnh huyền dài 10 cm. Tính diện tích của tam giác này.
Hướng dẫn giải:
Cạnh huyền aₕ=10 cm. Trong tam giác vuông cân, cạnh huyền có công thức: aₕ = a√2
Giải để tìm cạnh góc vuông a: a = aₕ / √2 = 10 / √2 = 10 × √2 / 2 = 5√2 ≈ 7.07 cm
Diện tích của tam giác vuông cân là: S = (a²) / 2 = (5√2)² / 2 = 50 / 2 = 25 cm²
Kết quả: Diện tích của tam giác vuông cân là 25 cm².
Bài tập 4: Tính chiều cao của tam giác vuông cân
Cho tam giác vuông cân có cạnh góc vuông dài 12 cm. Tính chiều cao của tam giác vuông cân này.
Hướng dẫn giải:
Chiều cao h của tam giác vuông cân tính từ đỉnh góc vuông xuống cạnh huyền có công thức: h = (a√2) / 2
Thay a =12:
h = (12√2) / 2 = 6√2 ≈ 8.49 cm
Kết quả: Chiều cao của tam giác vuông cân là khoảng 8.49cm.
Bài tập 5: Tính diện tích hình vuông khi biết đường chéo
Cho một hình vuông có đường chéo dài 14 cm. Hãy tính diện tích của hình vuông này.
Hướng dẫn giải:
Đường chéo của hình vuông chia hình vuông thành hai tam giác vuông cân.
Cạnh của hình vuông a sẽ bằng: a = √2 × đường chéo = √2 × 14 = 14 × √2 / 2 = 7√2 ≈ 9.90 cm
Diện tích hình vuông: S = a² = (7√2)² = 49 × 2 = 98 cm²
Kết quả: Diện tích hình vuông là 98cm2.
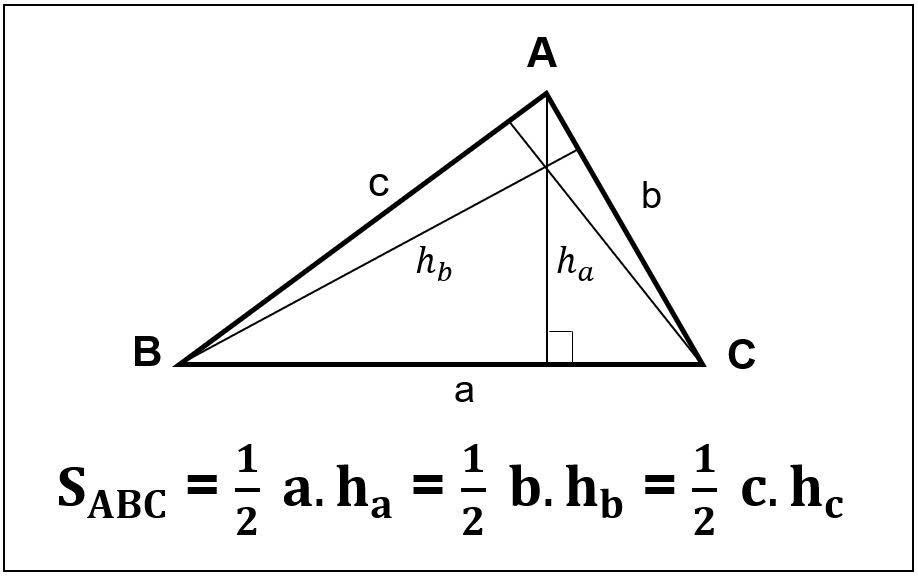Các bài tập áp dụng Diện tích của tam giác vuông cânTam giác vuông cân có rất nhiều ứng dụng trong thực tế, đặc biệt là trong các lĩnh vực liên quan đến xây dựng, thiết kế, vật lý và toán học. Dưới đây là một số ví dụ cụ thể:
1. Xây dựng và kiến trúc
Trong ngành xây dựng, tam giác vuông cân được sử dụng rộng rãi trong việc thiết kế các công trình, đặc biệt khi thiết kế các mái nhà, cầu thang, hoặc các cấu trúc hình học có tính đối xứng.
Mái nhà và mái vòm: Trong các mái nhà hình tam giác, các cấu trúc thường có các góc vuông và hai cạnh vuông bằng nhau, vì vậy diện tích của các hình tam giác vuông cân sẽ giúp tính toán vật liệu cần thiết.
Cầu thang: Khi thiết kế cầu thang vuông góc, chiều cao và chiều dài của các bậc thang thường tạo thành tam giác vuông cân. Diện tích của tam giác này có thể giúp tính toán diện tích mặt cầu thang.
2. Thiết kế đồ họa và nghệ thuật
Trong thiết kế đồ họa, các hình dạng vuông và tam giác vuông cân là các hình cơ bản. Việc tính toán diện tích của chúng là cần thiết khi thiết kế các tác phẩm, bao gồm cả việc xác định vị trí và tỷ lệ của các yếu tố trong thiết kế.
Lý thuyết hình học: Tam giác vuông cân là cơ sở để thiết kế các đối tượng hình học đơn giản, như các mẫu trang trí, biểu tượng hoặc logo trong thiết kế đồ họa.
Tỷ lệ vàng: Trong thiết kế và nghệ thuật, tam giác vuông cân có thể được sử dụng để thiết lập các tỷ lệ đối xứng, từ đó tạo ra các tác phẩm cân đối và hài hòa.
3. Vật lý và khoa học
Trong vật lý, tam giác vuông cân xuất hiện trong nhiều bài toán tính toán, đặc biệt là khi giải các bài toán liên quan đến vận tốc, lực, hoặc điện từ.
Điện từ học: Các bài toán liên quan đến điện trường và từ trường trong các trường hợp đối xứng có thể sử dụng hình tam giác vuông cân để tính toán diện tích và mô phỏng sự phân bố của các lực.
Vật lý cơ học: Khi giải bài toán chuyển động, tam giác vuông cân giúp mô phỏng các hiện tượng như chuyển động ngang và dọc. Diện tích tam giác được sử dụng trong các công thức để tính toán khoảng cách và thời gian.
4. Toán học và học thuật
Giải tích hình học: Tam giác vuông cân là một phần quan trọng trong các bài toán giải tích hình học, giúp học sinh và sinh viên hiểu rõ các công thức về diện tích, chu vi, và các đặc điểm hình học của tam giác vuông cân.
Ứng dụng trong lượng giác: Các tam giác vuông cân có tỷ lệ góc đặc biệt (45°-45°-90°), điều này rất quan trọng trong các bài toán lượng giác và ứng dụng thực tế liên quan đến các phép toán với sin, cos, tan.
5. Thiết kế kỹ thuật và chế tạo
Trong lĩnh vực chế tạo cơ khí và kỹ thuật, tam giác vuông cân được sử dụng trong việc thiết kế các chi tiết máy móc hoặc các bộ phận đối xứng.
Máy móc và công cụ: Các bộ phận của máy móc có thể được thiết kế dưới dạng tam giác vuông cân để tiết kiệm không gian và tối ưu hóa hiệu suất. Việc tính diện tích của tam giác vuông cân giúp xác định vật liệu và thiết kế chính xác.
Khảo sát địa chất: Trong khảo sát địa lý và xây dựng công trình, tam giác vuông cân có thể được sử dụng trong việc đo lường và xác định các góc, chiều cao, và khoảng cách.
6. Các bài toán thực tế liên quan đến đất đai và bất động sản
Khi tính toán diện tích đất đai hoặc thiết kế các khu đất có dạng tam giác vuông cân, việc áp dụng công thức diện tích của tam giác vuông cân giúp ước tính diện tích chính xác, từ đó hỗ trợ việc phân chia đất đai, tính toán chi phí xây dựng và các công việc liên quan.
Qua bài viết trên, chúng ta đã hiểu rõ về công thức và cách tính diện tích của tam giác vuông cân, cũng như những ứng dụng thực tế của nó trong đời sống và các lĩnh vực khác nhau như xây dựng, thiết kế, khoa học và kỹ thuật. Việc nắm vững kiến thức về diện tích của tam giác vuông cân không chỉ giúp chúng ta giải quyết các bài toán toán học một cách hiệu quả mà còn ứng dụng vào thực tế để tối ưu hóa công việc và nâng cao khả năng tính toán trong nhiều ngành nghề. Hy vọng bài viết đã mang lại cho bạn cái nhìn tổng quan và hữu ích về khái niệm này.
Nếu bạn cần thêm thông tin về dịch vụ marketing, hãy liên hệ với Kinh Bắc Media. Chúng tôi cung cấp các giải pháp marketing toàn diện, từ truyền thông trực tuyến, quảng cáo, đến xây dựng thương hiệu, nhằm giúp doanh nghiệp của bạn phát triển mạnh mẽ trong thị trường cạnh tranh. Đội ngũ chuyên gia của chúng tôi luôn sẵn sàng hỗ trợ và tư vấn để đáp ứng mọi nhu cầu của bạn.
Thông tin chi tiết vui lòng liên hệ:
Kinh Bắc Media
Địa chỉ: Tầng 4 tòa nhà Thanh Long số nhà 134 Mai Anh Tuấn - Hồ Hoàng Cầu - Đống Đa - Hà Nội
Hotline: 0969 024 600 / 024 62 733 721