Hệ thức lượng trong tam giác vuông
Hệ thức lượng tam giác vuông là một phần quan trọng trong hình học, giúp chúng ta tính toán các cạnh và góc của tam giác vuông. Dưới đây là một số lý thuyết cơ bản về hệ thức lượng tam giác vuông:
Định lý Pythagoras là một định lý nổi tiếng trong tam giác vuông. Nó phát biểu rằng:
Trong một tam giác vuông, bình phương của cạnh huyền (cạnh đối diện góc vuông) bằng tổng bình phương của hai cạnh góc vuông.
Công thức:
a² + b² = c²
Trong đó:
- a và b là các cạnh góc vuông (hai cạnh vuông góc với nhau),
- c là cạnh huyền (cạnh đối diện góc vuông).
Định lý Pythagoras giúp tính được một trong các cạnh nếu biết hai cạnh còn lại trong tam giác vuông.
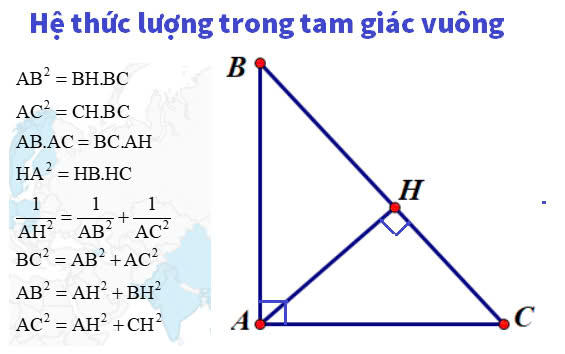Lý thuyết về hệ thức lượng tam giác vuôngTrong tam giác vuông, các tỉ số lượng giác (sin, cos, tan) mô tả mối quan hệ giữa các cạnh của tam giác và góc của nó.
Sin (sinus) của một góc θ trong tam giác vuông được định nghĩa là tỉ số giữa cạnh đối diện góc đó và cạnh huyền:
sin(θ) = cạnh đối / cạnh huyền = a / c
Cos (cosinus) của một góc θ trong tam giác vuông được định nghĩa là tỉ số giữa cạnh kề và cạnh huyền:
cos(θ) = cạnh kề / cạnh huyền = b / c
Tan (tangens) của một góc θ trong tam giác vuông được định nghĩa là tỉ số giữa cạnh đối và cạnh kề:
tan(θ) = cạnh kề / cạnh đối = b / a
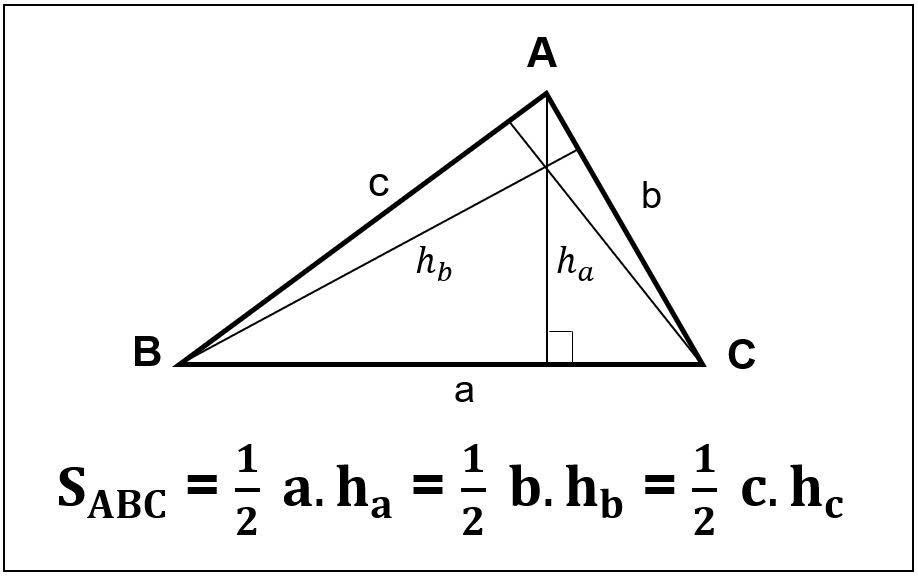
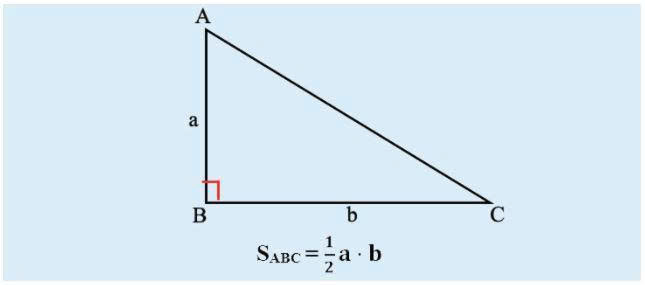
Diện tích của tam giác vuông có thể tính dễ dàng bằng công thức:
diện tích = 1/2 × a × b
Trong đó:
a và b là hai cạnh góc vuông của tam giác.
Công thức tính diện tích tam giác vuông
Chu vi của tam giác vuông được tính bằng tổng độ dài ba cạnh của nó:
Chu vi= a + b + c
Trong đó:
a và b là các cạnh góc vuông,
c là cạnh huyền.
Hệ thức lượng tam giác vuông có nhiều ứng dụng trong giải các bài toán hình học, đặc biệt là trong việc:
Tính toán các cạnh và góc khi biết một số yếu tố trong tam giác vuông.
Giải các bài toán về diện tích, chu vi của tam giác vuông.
Xác định các góc trong tam giác vuông thông qua các tỉ số lượng giác (sin, cos, tan).
Ứng dụng trong các bài toán thực tế, chẳng hạn như trong xây dựng, đo đạc, và vật lý.
Hệ thức lượng tam giác vuông cung cấp những công thức và tỉ số cơ bản giúp giải quyết nhiều vấn đề về hình học và lượng giác trong tam giác vuông. Những hệ thức này rất hữu ích trong việc tính toán các yếu tố còn thiếu khi đã biết một số thông số của tam giác.
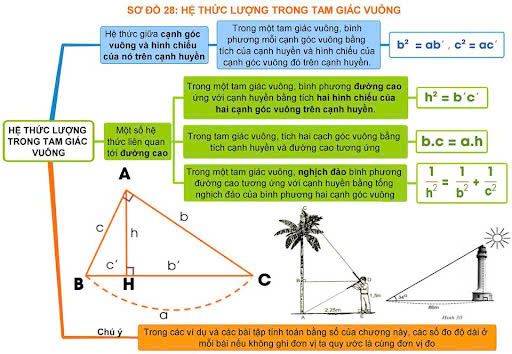một số bài tập về hệ thức lượng tam giác vuôngDưới đây là một số bài tập về hệ thức lượng tam giác vuông giúp bạn luyện tập:
Bài tập 1: Sử dụng Định lý Pythagoras
Cho tam giác vuông ABC, trong đó:
Cạnh AB=6 cm
Cạnh AC==8 cm Tính cạnh huyền BC.
Giải: Áp dụng Định lý Pythagoras:
BC² = AB² + AC² = 6² + 8² = 36 + 64 = 100
BC = √100 = 10 cm
Bài tập 2: Tính góc trong tam giác vuông
Cho tam giác vuông ABC, trong đó:
Cạnh AB=3 cm
Cạnh AC=4 cm Tính góc θ(góc giữa cạnh AB và cạnh huyền BC).
Giải: Áp dụng tỉ số lượng giác:
tan(θ) = AB / AC = 3/4
θ = tan⁻¹(3 / 4) ≈ 36.87°
Tính góc trong tam giác vuôngBài tập 3: Tính diện tích tam giác vuông
Cho tam giác vuông ABC, trong đó:
Cạnh AB=5 cm
Cạnh AC=12 cm Tính diện tích của tam giác.
Giải: Áp dụng công thức diện tích tam giác vuông:
diện tích = 1/2 × AB × AC = 1/2 × 5 × 12 = 30 cm²
Bài tập 4: Tính chu vi tam giác vuông
Cho tam giác vuông ABC, trong đó:
Cạnh AB=9 cm
Cạnh AC=12 cm Tính chu vi tam giác.
Giải: Áp dụng Định lý Pythagoras để tính cạnh huyền BC:
BC² = AB² + AC² = 9² + 12² = 81 + 144 = 225
BC = √225 = 15 cm
Sau đó, tính chu vi:
Chu vi=AB+AC+BC=9+12+15=36 cm
Bài tập 5: Tính một cạnh trong tam giác vuông
Cho tam giác vuông ABC, trong đó:
Cạnh huyền BC=13 cm
Cạnh AB=5 cm Tính cạnh còn lại AC.
Giải: Áp dụng Định lý Pythagoras:
BC² = AB² + AC²
13² = 5² + AC²
169 = 25 + AC²
AC² = 169 - 25 = 144
AC = √144 = 12 cm
Tính một góc trong tam giác vuôngBài tập 6: Tính một góc trong tam giác vuông
Cho tam giác vuông ABC, trong đó:
Cạnh AB=7cm
Cạnh BC=24cm Tính góc θ giữa cạnh AB và cạnh huyền BC.
Giải: Áp dụng tỉ số lượng giác:
sin(θ) = AB / BC = 7 / 24
θ = sin⁻¹(7 / 24) ≈ 16.26°
Qua bài viết trên, chúng ta có thể thấy rằng hệ thức lượng tam giác vuông không chỉ là kiến thức cơ bản trong hình học mà còn là công cụ quan trọng giúp giải quyết nhiều bài toán thực tế và lý thuyết. Các công thức như Định lý Pythagoras và các tỉ số lượng giác (sin, cos, tan) cung cấp cho chúng ta những mối quan hệ chặt chẽ giữa các cạnh và góc trong tam giác vuông. Việc nắm vững và ứng dụng đúng các hệ thức lượng này sẽ giúp chúng ta giải quyết các bài toán nhanh chóng và chính xác, đồng thời mở rộng khả năng ứng dụng trong nhiều lĩnh vực như vật lý, kỹ thuật và đo đạc. Vì vậy, hiểu và thành thạo các hệ thức lượng tam giác vuông là một phần không thể thiếu trong quá trình học tập và phát triển tư duy logic của mỗi người. Hy vọng các bài tập trên sẽ giúp bạn hiểu rõ hơn về cách áp dụng hệ thức lượng tam giác vuông.
Nếu bạn cần thêm thông tin về dịch vụ marketing, hãy liên hệ với Kinh Bắc Media. Chúng tôi sẵn sàng hỗ trợ bạn với các giải pháp tiếp thị chuyên nghiệp và hiệu quả, giúp bạn đạt được mục tiêu kinh doanh và nâng cao nhận diện thương hiệu.
Thông tin chi tiết vui lòng liên hệ:
Kinh Bắc Media
Địa chỉ: Tầng 4 tòa nhà Thanh Long số nhà 134 Mai Anh Tuấn - Hồ Hoàng Cầu - Đống Đa - Hà Nội
Hotline: 0969 024 600 / 024 62 733 721